Metrika
adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut
baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks
disebut dengan elemen atau anggota matriks. Dengan representasi matriks,
perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya
misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan
lainnya. Matriks seperti halnya variabel biasa dapat dikalkulasi,
seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.

ORDO
Ordo suatu matriks adalah bilangan yang menunjukkan banyaknya baris (m) dan banyaknya kolom (n).
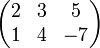 Matriks di atas berordo 2x3.
Matriks di atas berordo 2x3.
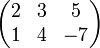 Matriks di atas berordo 2x3.
Matriks di atas berordo 2x3.MATRIKS TRANSPOS
Matriks transpose adalah matriks yang mengalami pertukaran elemen dari baris menjadi kolom dan sebaliknya.
CONTOH
 maka matriks transposenya (At) adalah
maka matriks transposenya (At) adalah
CONTOH
 maka matriks transposenya (At) adalah
maka matriks transposenya (At) adalah
KESAMAAN MATRIKS
Penjumlahan dan pengurangan matriks

Dua matriks A dan B dikatakan sama (ditulis A = B), jika
a. Ordonya sama
b. Elemen-elemen yang seletak sama
Contoh:

Tentukan nilai 2x-y+5z!
Jawab:
b. Elemen-elemen yang seletak sama
Contoh:

Tentukan nilai 2x-y+5z!
Jawab:
 maka
maka 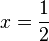
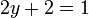 maka
maka 
 maka
maka 
Penjumlahan dan pengurangan matriks
Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki ukuran atau ordo yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
atau dalam representasi dekoratfinya
- Perkalian Skalar
- Matriks dapat dikalikan dengan sebuah skalar.
- Contoh perhitungan :
Matriks
dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom,
lalu dijumlahkan pada baris yang sama. Namun dengan syarat, dua matriks A
dan B terdefinisi untuk dikalikan, jikabanyaknya kolom A = banyaknya baris B, dengan hasil suatu matriks C yang berukuran (memiliki ordo) baris A x kolom B.Jika
syarat tersebut tidak dipenuhi (jumlah kolom matriks A tidak sama
dengan jumlah bari matriks B) maka kedua matriks tersebut tidak dapat
dikalikan.
A m x n x B n x p = C m x p
(jumlah kolom matriks A sama dengan jumlah baris kolom B yaitu n)
Contoh perhitungan :

diatas adalah matriks 2x3 dikali matriks 3x2 yang hasilnya adalah matriks 2x2.
Ket :
perkalian matriks bersifat tidak komutatif (AxB tidak sama dengan BxA) tetapi bersifatasosiatif (AxB)xC = Ax(BxC).
MATRIKS SATUANdiatas adalah matriks 2x3 dikali matriks 3x2 yang hasilnya adalah matriks 2x2.
Ket :
perkalian matriks bersifat tidak komutatif (AxB tidak sama dengan BxA) tetapi bersifatasosiatif (AxB)xC = Ax(BxC).
Matriks satuan adalah suatu matriks bujur sangkar, yang semua elemen diagonal utamanya adalah 1, sedangkan elemen lainya adalah 0.
Notasi : I (Identitas)

SIFAT AI = IA = A

SIFAT AI = IA = A
DETERMINAN MATRIKSMATRIKS ORDO 2X2
Misalkan:

maka Determinan A (ditulis ) adalah:
) adalah:

MATRIKS ORDO 3X3
CARA SARRUS
Misalkan:
Jika
 maka tentukan
maka tentukan  !
!

Penghitungan matriks dilakukan dengan cara menambahkan elemen dari kiri atas ke kanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) lalu dikurangi dengan elemen dari kanan atas ke kiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i) sehingga menjadi:
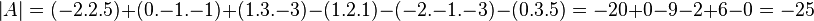
Contoh:
 maka tentukan
maka tentukan  !
!

CARA EKSPANSI BARIS KOLOM
Misalkan:
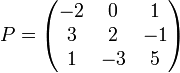
maka tentukan dengan ekspansi baris pertama!
dengan ekspansi baris pertama!

Misalkan:

maka Determinan A (ditulis
 ) adalah:
) adalah:
MATRIKS ORDO 3X3
CARA SARRUS
Misalkan:
Jika
 maka tentukan
maka tentukan  !
!
Penghitungan matriks dilakukan dengan cara menambahkan elemen dari kiri atas ke kanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) lalu dikurangi dengan elemen dari kanan atas ke kiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i) sehingga menjadi:
Contoh:
 maka tentukan
maka tentukan  !
!
CARA EKSPANSI BARIS KOLOM
Misalkan:
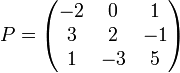
maka tentukan
 dengan ekspansi baris pertama!
dengan ekspansi baris pertama!
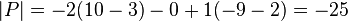
MATRIKS SINGULAR Matriks singular adalah matriks yang nilai determinannya 0.
Contoh:
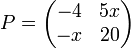
Jika A matriks singular, tentukan nilai x!
Jawab:
MATRIKS INVERSMisalkan: maka inversnya adalah:
maka inversnya adalah:

1. (At)t = A
2. (A + B)t = At + Bt
3. (A . B)t = Bt . At
4. (A . B)-1 = B-1 . A-15. A . A-1 = A-1 . A = I
Persamaan matriks
Tentukan X matriks dari persamaan:
Contoh:
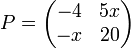
Jika A matriks singular, tentukan nilai x!
Jawab:


 vs
vs 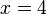
MATRIKS INVERSMisalkan:
 maka inversnya adalah:
maka inversnya adalah:

- Bilangan (ad-bc) disebut determinan dari matriks A
- Matriks A mempunyai invers jika Determinan A ¹ 0 dan disebut matriks non singular.
1. (At)t = A
2. (A + B)t = At + Bt
3. (A . B)t = Bt . At
4. (A . B)-1 = B-1 . A-15. A . A-1 = A-1 . A = I
Persamaan matriks
Tentukan X matriks dari persamaan:
- Jika diketahui matriks A.X=B
- Jika diketahui matriks X.A=B








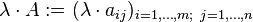


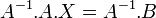






0 Response to "Matriks"
Post a Comment